Find the center (h, k) and the radius r of the circle.x2 + y2 - 4x - 12y + 25 = 0
A. (h, k) = (2, 6), r =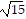 
B. (h, k) = (-2, -6), r = 15
C. (h, k) = (2, 6), r = 15
D. (h, k) = (-2, -6), r =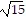 
Answer: A
You might also like to view...
Find the power of i.i46
A. 1 B. -i C. -1 D. i
Graph the function.f(x) = 3x
A.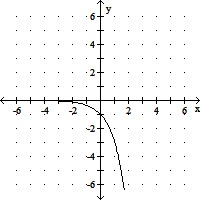 
B.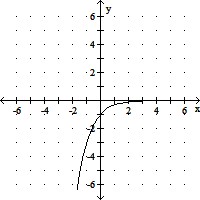 
C.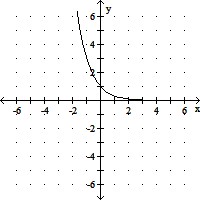 
D.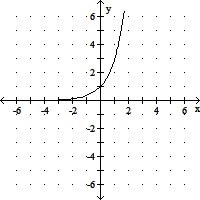 
Rewrite the system of inequalities, adding slack variables or subtracting surplus variables as needed.2x1 + x3 ? 562x1 + x2 ? 34 x1 + x3 ? 28
A. 2x1 + x3 - s1 = 56 2x1 + x2 + s2 = 34 x1 + x3 + s3 = 28 B. 2x1 + x3 - s1 = 56 2x1 + x2 - s2 = 34 x1 + x3 - s3 = 28 C. 2x1 + x3 + s1 = 56 2x1 + x2 + s2 = 34 x1 + x3 + s3 = 28 D. 2x1 + x3 + s1 = 56 2x1 + x2 - s2 = 34 x1 + x3 - s3 = 28
Solve the problem.A drug is injected into a patient and the concentration of the drug is monitored. The drug's concentration, C(t), in milligrams after t hours is modeled by C(t) =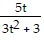 
.What is the end behavior of this function? Describe what this means in practical terms.
A. as x ? ?, C(x) ? 0; 0 is the final amount, in milligrams, of the drug that will be left in the patient's bloodstream. B. as x ? ?, C(x) ? 1.67; After 1.67 hours, the concentration of the drug is at its greatest. C. as x ? ?, C(x) ? 0.83; After 0.83 hours, the concentration of the drug is at its greatest. D. as x ? ?, C(x) ? 1.67; 1.67 is the final amount, in milligrams, of the drug that will be left in the patient's bloodstream.