If a circle O has radius r and arc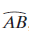 
of circle O has a central angle of 18°, then
(a) the ratio of the length of 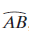to the area of sector AOB is 1:2.
(b) if P is on circle O,?APB = 18°.
(c) ?AOB = 9°.
(d) the ratio of the minor arc 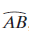to the major arc 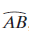is 1:20.
(e) None of these is correct.
(a) the ratio of the length of 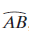to the area of sector AOB is 1:2.
You might also like to view...
A certain animal grows to a maximum length of 28 inches. Its length, in inches, at age src="https://sciemce.com/media/3/ppg__cognero__Section_6.4_Equations_of_Change_Linear_and_Exponential_Functions__media__880d031b-fe53-4676-9f4b-a6ab67b6d679.PNG" class="wirisformula" align="middle" style="vertical-align: middle;" data-wiris-created="true" varid="variable_id_field" variablename="impvar_a1f2bc38aca54c8a9e58b15b3" /> between the maximum length and the current length satisfies the equation of change
years is given by the function 
. The difference
.
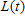
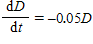
A: If the animal is 5 inches long when it is born, find a formula that gives the length difference D as a function of the age t. Write your answer using the alternative form for an exponential function.B: Find a formula that gives the length in terms of the age.C: What is the animal's length at age 8 years?
What will be an ideal response?
Evaluate the geometric series or state that it diverges.
A. 3 B. 2 C. 1 D. 6
Solve.Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The income from the 5% and 6% investments is the same as the income from the 8% investment. Find the amount invested at each rate.
A. At 5%: $5000; at 6%: $10,000; at 8%: $10,000 B. At 5%: $8000; at 6%: $10,000; at 8%: $7000 C. At 5%: $10,000; at 6%: $10,000; at 8%: $5000 D. At 5%: $10,000; at 6%: $5000; at 8%: $10,000
Simplify using the quotient rule.
A. -5x6y7 B. -5x7y3 C. -5x6y2 D. x7y3