Solve the problem.Find the equation of the parabola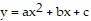 
that passes through the points (-2, 4), (0, -2), and (3, 1).
A. y =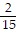 
x2 + 1x - 5
B. y =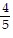 
x2 - 
x - 2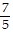
C. y = - 
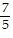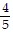x2 + 
x - 2
D. y =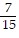 
x2 - 
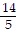x - 
Answer: B
You might also like to view...
Provide an appropriate response.Describe how the graph of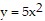 
differs from the graph of 
.
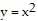What will be an ideal response?
Create the requested display.The traveling times in minutes for 15 workers randomly chosen at an office are: 55, 40, 35, 30, 50, 45, 25, 15, 50, 45, 35, 30, 45, 50, 45Create a dotplot of the data.
What will be an ideal response?
Solve the problem.Suppose that an insect population density, in thousands, during year n can be modeled by the recursively defined sequence: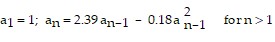 
.Use technology to graph the sequence for n = 1 , 2 , 3 , ........., 20 . Describe what happens to the population density function.
A. The insect population stabilizes near 4.52 thousand. B. The insect population stabilizes near 7.72 thousand. C. The insect population stabilizes near 7.18 thousand. D. The insect population increases every year.
Simplify the radical expression by factoring out the largest perfect nth power. Assume that all variables are positive.-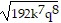 
A. 8k7q8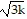
B. 8k3q4
C. -8k3q4
D. -8k3q4