Complete the table and numerically estimate the limit as x approaches infinity for  .
.
x
100
101
102
103
104
105
106
f(x)
?
?
A. 0
| x | 100 | 101 | 102 | 103 | 104 | 105 | 106 |
| f(x) | -3 | -0.723805 | -0.074972 | -0.0075 | -0.00075 | -0.000075 | ? -0.000008 |
B. 15
| x | 100 | 101 | 102 | 103 | 104 | 105 | 106 |
| f(x) | -3 | -0.723805 | -0.074972 | -0.0075 | -0.00075 | -0.000075 | ?-0.000008 |
C. -15
| x | 100 | 101 | 102 | 103 | 104 | 105 | 106 |
| f(x) | -0.000008 | -0.000075 | -0.00075 | -0.0075 | -0.074972 | -0.723805 | -3? |
D. ?
| x | 100 | 101 | 102 | 103 | 104 | 105 | 106 |
| f(x) | -0.000008 | -0.000075 | -0.00075 | -0.0075 | -0.074972 | -0.723805 | -3? |
E. does not exist
| x | 100 | 101 | 102 | 103 | 104 | 105 | 106 |
| f(x) | does not exist | does not exist | does not exist | does not exist | does not exist | does not exist | ?does not exist |
Answer: A
You might also like to view...
Solve the problem.Two airplanes depart from the same place at 3:00 p.m. One plane flies north at a speed of 423 km/hr, and the other flies east at a speed of 500 km/hr. How far apart are the airplanes at 6:00 p.m.? Round your answer to the nearest tenth if necessary.
A. 654.9 km B. 3,860,361.0 km C. 1964.8 km D. 2,680,806.3 km
Graph the solution of the system of linear inequalities.
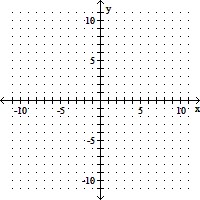
A. 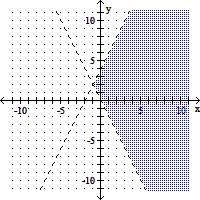
B. 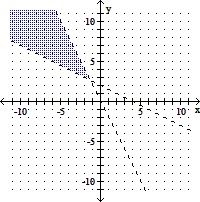
C. 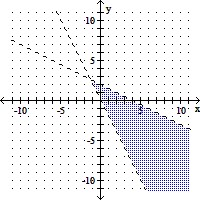
D. 
Write the number in words.3072
A. Three hundred thousand, seventy-two B. Three million, seventy-two C. Three thousand, seventy-two D. Thirty thousand, seventy-two
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. Determine where the function is increasing and where it is decreasing. If necessary, round answers to two decimal places.f(x) = -0.3x3 + 0.2x2 + 4x - 5; (-4, 5)
A. local maximum at (-1.9, -9.82) local minimum at (2.34, 1.61) increasing on [-1.9, 2.34] decreasing on [-4, -1.9] and [2.34, 5] B. local maximum at (2.34, 1.61) local minimum at (-1.9, -9.82) increasing on [-4, -1.9] and [2.34, 5] decreasing on [-1.9, 2.34] C. local maximum at (2.34, 1.61) local minimum at (-1.9, -9.82) increasing on [-1.9, 2.34] decreasing on [-4, -1.9] and [2.34, 5] D. local maximum at (-1.9, -9.82) local minimum at (2.34, 1.61) increasing on [-4, -1.9] and [2.34, 5] decreasing on [-1.9, 2.34]