The radius of a horizontal curve on an existing highway was field-measured to be 810 ft. The pavement on this two-lane highway is 22 ft wide, and the elevation difference between the inside and outside of the curve is 1.43 ft. The posted speed limit on the road is 60 mi/h. Is this a hazardous location? If so, why? What action will you recommend to correct the situation?
What will be an ideal response?
Assume that the design speed of this section of roadway is 70 mi/h (10 mi/h above the posted speed limit). Next, determine the coefficient of side friction, fs, from Table 3.3. fs = 0.10
Next, determine the rate of superelevation, e:
e = 1.43/22
e = 0.065
Next, determine the maximum permissible speed on this existing curve by using equation 3.34.
R = u2 / 15(e + fs)
u2 = 15(R)(e + fs)
u = [15(810)(0.065 + 0.10)]1/2
u = 44.77 mi/h
This curve is hazardous since the speed limit is posted at 60 mi/h yet the maximum safe speed in the curve is approximately 45 mi/h. One low cost measure to increase the safety of this curve would be to reduce the speed limit to 45 mi/h, or to post a curve warning sign with an advisory (maximum safe) speed of 45 mi/h. A long-term solution to improve safety would be to increase the radius of curvature to permit safe operation at the speed limit. This can be accomplished by using the above equation (equation 3.34):
R = (60)2 / 15(0.065 + 0.10)
R = 1,454.54 ft.
Therefore, to permit safe travel at the maximum speed limit, the radius of the curve should be increased to 1,455 feet.
You might also like to view...
Primary tillage can be performed with which of the following?
a. cultivator c. harrow b. rotary hoe d. moldboard plow
The __________________ ports located in the piston chambers help vent the brake fluid back into the reservoirs.
A. compensating B. relief C. dump D. pressure
? Identify and state the historical significance of St. Augustine, Florida.
What will be an ideal response?
(a) F 5 = 3000(F/A,10%,4) = 3000(4.6410) = $13,923 (b) F 4 = 3000[(F/A,10%,3) + (P/F,10%,1)] = 3000[3.3100 + 0.9091] = $12,657
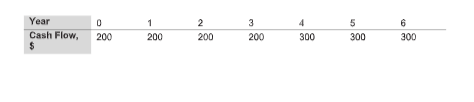
What will be an ideal response?