Solve the problem.For x > 0, sketch a curve y = f(x) that has f(1) = 0 and f'(x) = - 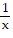 . Can anything be said about the concavity of such a curve? Give reasons for your answer.
. Can anything be said about the concavity of such a curve? Give reasons for your answer.
What will be an ideal response?
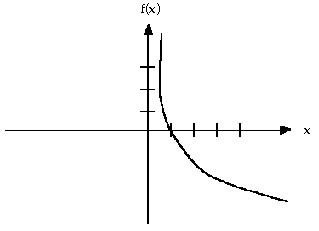
Since f''(x) = 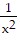 > 0 for all x > 0, then the function is everywhere concave up.
> 0 for all x > 0, then the function is everywhere concave up.
You might also like to view...
Find the first four terms of the binomial series for the given function.(1 - 6x)1/2
A. 1 + 3x +  x2 -
x2 - 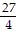 x3
x3
B. 1 - 3x - 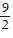 x2 -
x2 - 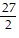 x3
x3
C. 1 - 3x - 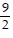 x2 -
x2 - 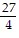 x3
x3
D. 1 - 3x + 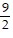 x2 -
x2 -  x3
x3
Answer the question.The graph below shows estimated world population for the period 4000 BC - 2000 AD. Note that the logarithm of the world population and not actual population is plotted on the vertical axis. This means, for example, that when the graph reaches 7 on the vertical scale, world population is 107 and when the graph reaches 9 on the vertical scale, world population is 109. Log World Population  ? -4000 -2000 0 2000Why must the graph be interpreted with care? If the graph is not interpreted with care what misleading impression might one have of world population during the period 4000 BC - 2000 AD? Why do
? -4000 -2000 0 2000Why must the graph be interpreted with care? If the graph is not interpreted with care what misleading impression might one have of world population during the period 4000 BC - 2000 AD? Why do
you think that the graph was presented in this form? What will be an ideal response?
If the diagonals of a parallelogram are congruent, then the parallelogram isa rhombus.
Answer the following statement true (T) or false (F)
Write the system of equations associated with the augmented matrix. Do not solve.
A. 4x + 3y + 8z = -9
| -8x + 3y | = 2 |
| 8x | - 9z = -2 |
B. 4x + 3y + 8z = -9
| -8x + | 3z = 2 |
| 8x - 9y | = -2 |
C. 4x + 3y + 8z = -9
| -8x + 3y | = 2 |
| 8x - 9y | = -2 |
D. 4x + 3y + 8z = -9
-8x + 3y + 2z = 0
8x - 9y - 2z = 0