Find the sum Sn of the first n terms of the geometric sequence. 3, -9, 27, -81, 243, . . . ; n = 10
A. -44,279
B. -44,286
C. -44,292
D. -44,288
Answer: B
You might also like to view...
Solve the equation.63 = 9k
A. 53 B. 7 C. 54 D. 6
Write the matrix equation as a system of linear equations without matrices.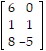
= 
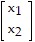A. 6x1 + x2 = -5 x1 + 7x2 = 7 8x1 - 5x2 = 6 B. 6x1 = -5 x1 + x2 = 7 8x1 - 5x2 = 6 C. 6x1 + x2 + x3 = -5 x1 - 5x2 = 7
Use the payoff matrix to determine the best strategy.A farmer must decide on which of two pieces of land to grow his crops. The first piece of land has better soil and will yield a larger harvest. However this piece of land is low lying and is coastal and his crops will be destroyed in the event of a storm and flooding. The second piece of land has poorer soil and will yield a smaller harvest but is at a higher elevation and would not be affected by flooding. He estimates that the payoff matrix is as follows:FloodingNo flooding
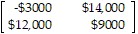Based on meteorological records from previous years,
the farmer estimates the probability of flooding next year to be 0.1. What is the farmer's best strategy? A. Use the land that is at a higher elevation B. Wait and see C. Use the land that is at a lower elevation
Solve the problem.Find a matrix A and a column matrix B that describe the following tables involving credits and tuition costs. Find the matrix product AB and interpret the significance of the entries of this product.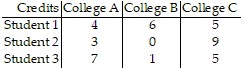
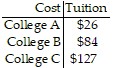
A.
AB =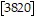 
The total tuition paid by all 3 students is $3820.
B.
AB =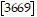 
The total tuition paid by all 3 students is $3669.
C.
AB =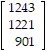 
Tuition for Student 1 is $1243, tuition for Student 2 is $1221, and tuition for Student 3 is $901.
D.
AB = 
Tuition for Student 1 is $1236, tuition for Student 2 is $1223, and tuition for Student 3 is $887.