How can we know that energy is conserved in a transformer? Explain
What will be an ideal response?
We give two possible explanations.
(1) We ask ourselves "Where could any energy that is lost have gone?" It can't go into the
magnetic field, because it is getting bigger and smaller with the alternating current. It can't
go to the current, because the charges are just "sloshing" back and forth with the
alternating current. The only place it can go is to Joule heat (and, indeed, some energy does
go to Joule heating). However, in practice, the loss is very small. Energy should be
conserved.
(2) As was seen in the section on transformers, each loop wrapped around an iron core
carrying an alternating current has the same potential difference (voltage) across it. Each
loop causes or is caused by a changing magnetic field. These fields all add together because
they all point in the same way. If I have 100 loops on one side, they can make the magnetic
field by adding together 100 little magnetic fields from each of the current loops. Suppose I
have only one loop on the other side. Those 100 loops could make quite a big magnetic
field all together, to make one equally big on the other side is going to require a much larger
change in current, so the current itself will have to be greater (by a factor of 100). More
loops, more voltage and less current needed to maintain the magnetic field; fewer loops, less
voltage and more current needed to maintain the magnetic field. In some sense, the current
trades off the voltage.
Consider a concrete example: the potential difference (voltage) across each loop is 1 V. The
product of voltage and current for the 100 loops is 100(1 V) x the current in a single loop
(call it i): (1 V) x i. The product of voltage and current for the single loop is (1 V) x (100i).
These numbers are the same, so the power on each side is the same, and power is the rate of
passage of energy through the transformer, so the energy is the same on each side—it is
conserved.
You might also like to view...
Exhibit 12-1
The figure below shows a graph of angular velocity versus time for a woman bicycling around a circular track.
?
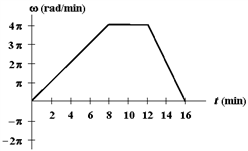
?
Use this exhibit to answer the following question(s).
Refer to . What is her angular displacement (in rad) in the first 12 minutes?
a.
0
b.
2?
c.
4?
d.
16?
e.
32?
About how fast are molecules in air moving?
A. 1 000 ft/sec B. the speed of light C. 9.8 m/sec D. 9.8 cm/sec
Spheres of Charge: A nonconducting sphere of mass 18.5 kg and diameter 25.0 cm has 8.10 × 1015 electrons removed from it. The points of removal are spread uniformly throughout the volume of this sphere. A tiny neutral plastic ball of mass 0.120 g is placed just outside the surface of the large sphere and is then released. How many electrons must be removed from the plastic ball so that its initial acceleration just after being released will be 1525 m/s2? You can neglect gravity. (e = 1.6 × 10-19 C, k = 1/4??0 = 8.99 × 109 N ? m2/C2)
Fill in the blank(s) with the appropriate word(s).
Mars's atmosphere is most similar in composition to the atmosphere of ________.
A. Mercury B. Venus C. the Moon D. Earth