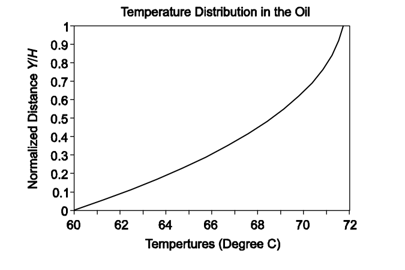
This is negative throughout the region, therefore, T(y) is concave down throughout the region and the temperature at y = 1.6 mm is indeed the maximum temperature. These calculations are verified by the graph of T(y). Inserting ymax into the expression for T(y) yields: Tmax = T(0.00161 mm) = 48.8°C.
GIVEN
A journal bearing
Diameter (D) = 100 mm = 0.1 m
Clearance (H) = 0.5 mm = 0.0005 m
Rotational speed (@) = 3600 rpm
Oil properties
? Density (p) = 800 kg/m3
? Viscosity (?) = 0.01 kg/ms
? Thermal conductivity (k) = 0.14 W/(m K)
Temperature of bearing surface (Tb) = 60°C
FIND
(a) Temperature distribution in the oil film
ASSUMPTIONS
Steady state
Uniform and constant bearing surface temperature
Constant fluid properties
The journal surface is insulated (negligible heat transfer)
SKETCH
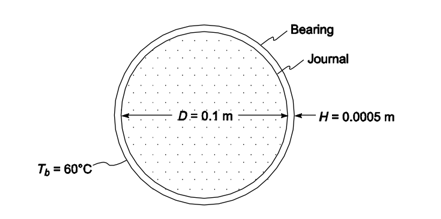
Since the clearance is small compared to the bearing diameter, the bearing may be idealized as parallel flat plates with oil between them, one stationary and one moving
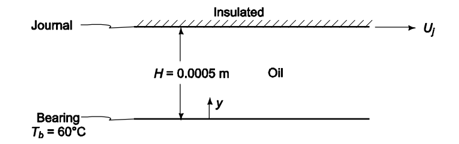
(a) As shown in Problem 5.20, the velocity distribution for this geometry is linear
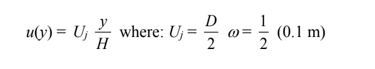
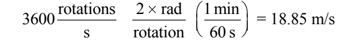
For this geometry, the energy Equation (5.6) with viscous dissipation reduces to
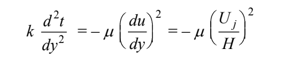
With boundary conditions: at y = 0 T = Tb
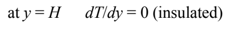
Integrating
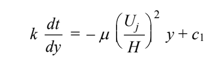
Applying the second boundary condition
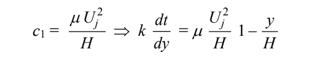
Integrating
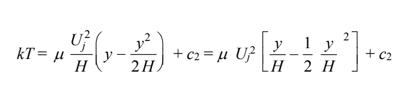
Applying the first boundary condition c2 = kTb
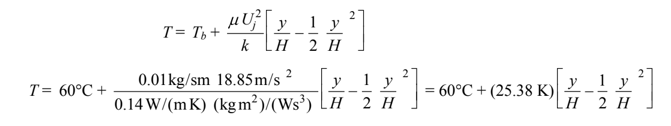
This is shown graphically below
You might also like to view...
How many valence electrons does boron (B, atomic no. = 5) have?
A) 1 B) 2 C) 3 D) 4 E) 5
Measurements of carbon dioxide concentrations in our atmosphere over the past 800,000 years show
A) an indirect correlation with global surface temperatures B) a direct correlation with global surface temperatures, only over the past century C) no correlation with global surface temperatures D) a direct correlation with global surface temperatures
550 g of water at 105°C are poured into an 855 g aluminum container with an initial temperature of 11°C. The specific heat of aluminum is 900 J/(kg•K)
How much heat flows from the water to the aluminum, assuming no heat is exchanged with the surroundings? A) 55 kJ B) 36 kJ C) 54 kJ D) 46 kJ E) 64 kJ
A mass m = 4.0 kg is connected, as shown, by a light cord to a mass M = 6.0 kg, which slides on a smooth horizontal surface. The pulley rotates about a frictionless axle and has a radius R = 0.12 m and a rotatinal inertia I = 0.090 kg?m2. The cord does not slip on the pulley. What is the magnitude of the acceleration of m?
?
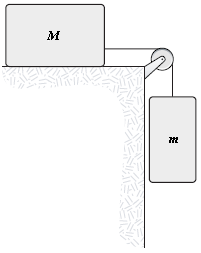
?
a.
?2.4 m/s2
b.
?2.8 m/s2
c.
?3.2 m/s2
d.
?4.2 m/s2
e.
?1.7 m/s2