Write the equation of the circle in standard form. Find the center and radius. Then sketch the graph.x2 + y2 + 2x - 48 = 0
A. (x - 1)2 + y2 = 49
(h, k) = (1, 0), r = 7
B. x2 + (y - 1)2 = 49
(h, k) = (0, 1), r = 7
C. (x + 1)2 + y2 = 49
(h, k) = (- 1, 0), r = 7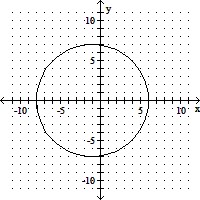
D. x2 + (y + 1)2 = 49
(h, k) = (0, - 1), r = 7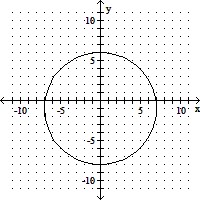
Answer: C
You might also like to view...
Solve the problem.The pressure of a gas varies jointly as the amount of the gas (measured in moles) and the temperature and inversely as the volume of the gas. If the pressure is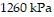 
(kiloPascals) when the number of moles is 4, the temperature is 
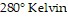, and the volume is 
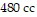, find the pressure when the number of moles is 6, the temperature is 
, and the
volume is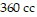 
.
A. 1215
B. 2250
C. 2340
D. 1170
A bag contains 6 cherry, 3 orange, and 2 lemon candies. You reach in and take 3 pieces of candy at random. Find the probability.2 orange, 1 lemon
A. .1091 B. .0303 C. .3636 D. .0364
Decide whether the given number is a solution of the given equation.Is 8 a solution of y + 12 = 20 ?
A. Yes B. No
Solve the problem.A scientist studying ocean tides places an 8 ft high marker in the water at 6 am on a Monday morning. At that time the water is about 5.5 ft high and receding. The scientist observes that the water reaches its lowest level, 0.1 ft, at 9:18 am and then begins to rise. Assume that the water level, in feet, is given by h(t) = 4.9 sin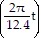
+ 5, where t represents the number of hours after midnight. (In other words, the marker was placed in the water when t = 6.) Find the first time interval during which the marker is completely underwater.
A. Approximately from 2:06 pm to 4:24 pm Monday B. Approximately from 1:42 pm to 5:18 pm Monday C. Approximately from 1:18 am to 4:54 am Tuesday D. Approximately from 11:24 pm Monday to 2:00 am Tuesday