Find the equation of the tangent plane (or tangent "hyperplane" for a function of three variables) at the given point p.f(x, y, z) = x2 + y2 + xyz, p = (-3, -4, 0)
A. w = -6x - 8y + 25
B. w = -6x - 8y - 25
C. w = -6x - 8y + 12z + 25
D. w = -6x - 8y + 12z - 25
Answer: D
You might also like to view...
Solve the problem.S and T are similar polygons. If the perimeter of S is 16, what is the perimeter of T?
A. 50 B. 40 C. 64 D. 80 E. none of these
Answer the question or provide the appropriate response.Explain how you would solve the following problem graphically. (Do not actually solve the problem.) If a rectangle has perimeter 74 inches, what is the maximum area that it can have? (Let x represent the width of the rectangle.)
A. Graph the function y = -x2 + 37x and find its x-intercepts. The larger x-intercept gives the maximum area (in square inches). B. Graph the function y = -x2 + 37x and find its vertex. The x-coordinate of the vertex gives the maximum area (in square inches). C. Graph the function y = -x2 + 37x and find its vertex. The y-coordinate of the vertex gives the maximum area (in square inches). D. Graph the function y = -x2 + 74x and find its vertex. The y-coordinate of the vertex gives the maximum area (in square inches).
Solve the problem.30 marbles are to be divided into three bags so that the second bag has three times as many marbles as the first bag and the third bag has twice as many as the first bag. If x is the number of marbles in the first bag, find the number of marbles in each bag.
A. 1st bag = 6 marbles; 2nd bag = 18 marbles; 3rd bag = 12 marbles B. 1st bag = 6 marbles; 2nd bag = 14 marbles; 3rd bag = 10 marbles C. 1st bag = 5 marbles; 2nd bag = 15 marbles; 3rd bag = 10 marbles D. 1st bag = 5 marbles; 2nd bag = 10 marbles; 3rd bag = 15 marbles
Solve the problem.On a summer day, the surface water of a lake is at a temperature of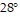 
Celsius. What is this temperature in Fahrenheit?
A. 60° B. 82.4° C. 50.4° D. 28°