Give the numerical coefficient of the term.-w
A. 0
B. -1
C. -w
D. 1
Answer: B
You might also like to view...
Find the values of a1, a2, a3, and a4.an = 
A. -1, 1, 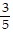 ,
, 
B. 1, 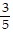 ,
, 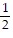 ,
, 
C.  ,
,  ,
, 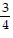 ,
, 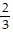
D. 0,  ,
, 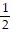 ,
, 
Factor the perfect square.49x2 + 56x + 16
A. (7x - 5)2 B. (7x + 4)(7x - 4) C. (7x + 4)2 D. (7x - 4)2
Rationalize the denominator.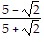
A. 
B. 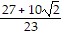
C. 
D. -1
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
If a1, a2, a3, ... , an and b1, b2, b3, ... , bn are geometric progressions, then a1 b1, a2 b2, a3 b3, ... , an bn is also a geometric progression. a. It is false. If a1, a2, a3, a4, ... = 1, 3, 6, 9,.. b1, b2, b3, b4, ... = 2, 4, 8, 16,.. are geometric progressions, then we can see that a1 b1, a2 b2, a3 b3, ... = 2, 12, 48, ... is not a geometric progression. b. It is true. A geometric progression is completely determined if the first term and the common ratio are known. Thus, if a1, a2, a3, ... , an , ... is a geometric progression with the first term given by a and common ratio given by r, then by definition, a1 = a a2 = a1 r = ar a3 = a2r = ar2 . . an = an-1 = ar n – 1 Thus, we see that the product of two nths terms of two geometric progressions is given by a n b n = a r n – 1 b where a,b are the first terms of these progressions and r, r1 are their common ratios respectively. Then we obtain that a1, b1, a2, b2, a3, b3, ... , an, bn is also geometric progression with first term ab and common ratio rr1.