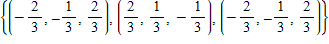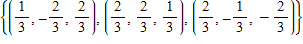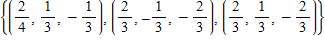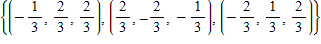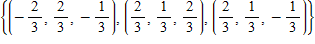?Use the Gram-Schmidt orthonormalization process to transform the basis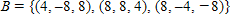 
for R?3 into an orthonormal basis. Use the Euclidean inner product for R?3 and use the vectors in the order in which they are shown.
?
A. ?
B. ?
C. ?
D. ?
E. ?
Answer: B
You might also like to view...
Find all real numbers that satisfy the equation.tan x = - 1
A.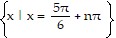 
B. 
C. 
D.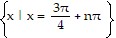 
Rewrite the expression as an equivalent expression that does not contain powers of trigonometric functions greater than 1.cos4 x
A. 
B.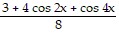 
C. 
D. 
Solve the equation.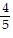
= 
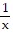
A.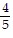 
B. 20
C.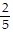 
D. 
Decide whether or not the points are the vertices of a right triangle.Consider the three points A = (7, 7), B = (9, 11), C = (11, 10). Determine whether the triangle ABC is a right triangle. Explain your reasoning.
A. The side lengths of triangle ABC are d(A, B) = 3
, d(A, C) = 5, d(B, C) = 
.
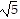[d(A, B)]2 + [d(B, C)]2 = (3
)2 + (
)2 = 18 + 5 = 23
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
B. The side lengths of triangle ABC are d(A, B) = 2
, d(A, C) = 5, d(B, C) = 
.
[d(A, B)]2 + [d(B, C)]2 = (2
)2 + (
)2 = 20 + 5 = 25
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
C. The side lengths of triangle ABC are d(A, B) = 2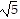
, d(A, C) = 2
, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2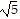
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = (2
)2 = 24
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
D. The side lengths of triangle ABC are d(A, B) = 2
, d(A, C) = 5, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.