Use the formula for the sum of the first n terms of a geometric sequence to solve.Find the sum of the first 10 terms of the geometric sequence: -6, -18, -54, -162, -486, . . . .
A. -177,164
B. -177,142
C. -177,144
D. -177,107
Answer: C
You might also like to view...
Complete.248 oz = cups
A. 62 B. 496 C. 31 D. 124
Using the addition/subtraction method, find the value of x and y to satisfy the following equations: x - 5y = 4; 2x - 3y = -6
a. x = 6 y = 2 b. x = -6 y = -2 c. x = -2 y = -6 d. x = 2 y = 6 e. x = -2 y = -2
Solve the formula for the specified letter.P = 
for r
A. r = P - tA
B. r = 
C. r =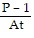 
D. r = 
Decide whether or not the points are the vertices of a right triangle.Consider the three points A = (7, 7), B = (9, 11), C = (11, 10). Determine whether the triangle ABC is a right triangle. Explain your reasoning.
A. The side lengths of triangle ABC are d(A, B) = 3
, d(A, C) = 5, d(B, C) = 
.
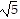[d(A, B)]2 + [d(B, C)]2 = (3
)2 + (
)2 = 18 + 5 = 23
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
B. The side lengths of triangle ABC are d(A, B) = 2
, d(A, C) = 5, d(B, C) = 
.
[d(A, B)]2 + [d(B, C)]2 = (2
)2 + (
)2 = 20 + 5 = 25
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
C. The side lengths of triangle ABC are d(A, B) = 2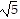
, d(A, C) = 2
, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2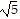
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = (2
)2 = 24
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
D. The side lengths of triangle ABC are d(A, B) = 2
, d(A, C) = 5, d(B, C) = 2.
[d(A, B)]2 + [d(B, C)]2 = (2
)2 + 22 = 20 + 4 = 24
[d(A, C)]2 = 52 = 25
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.