Solve the problem.The following equations each describe the motion of a particle. For which path is the particle's velocity vector always orthogonal to its acceleration vector?(1) r(t) = t3i + t6j(2) r(t) = cos (2t)i + sin (6t)j(3) r(t) = ti + tj(4) r(t) = cos (9t)i + sin (9t)j
A. Path (3)
B. Path (2) and Path (4)
C. Path (4)
D. Path (1)
Answer: C
You might also like to view...
Use power series operations to find the Taylor series at x = 0 for the given function.x6 cos ?x
A.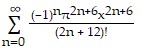 
B.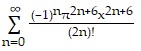 
C.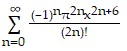 
D.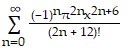 
Perform the indicated operations. Leave the result in polar form.[2(cos 90° + j sin 90°)][5(cos 200° + j sin 200°)]
A. 10(cos 18,000° + j sin 18,000°) B. 7(cos 290° + j sin 290°) C. 7(cos 18,000° + j sin 18,000°) D. 10(cos 290° + j sin 290°)
Plot and interpret the appropriate scatter diagram.The table gives the times spent watching TV and the grades of several students. 
Effect of Watching TV on Grades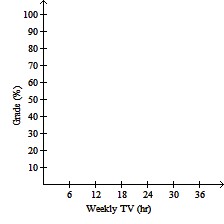 
A. Effect of Watching TV on Grades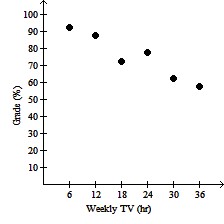
More hours spent watching TV may
increase grades.
B. Effect of Watching TV on Grades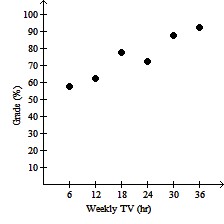
More hours spent watching TV may
increase grades.
C. Effect of Watching TV on Grades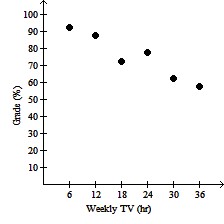
More hours spent watching TV may
reduce grades.
D. Effect of Watching TV on Grades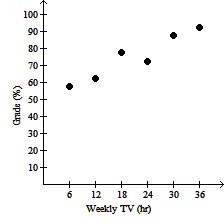
More hours spent watching TV may
reduce grades.
Factor the GCF out of the given expression.x(x - 8) - 9(x - 8)
A. (x + 9)(x + 8) B. (x + 9)(x - 8) C. (x - 9)(x - 8) D. (x - 9)(x + 8)