Use Cramer’s Rule to solve (if possible) the system of equations.
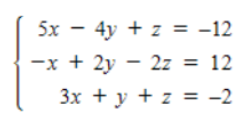
a. (0, 2, –4)
b. (0, –2, 4)
c. (0, –2, –4)
d. (0, 2, 4)
a. (0, 2, –4)
You might also like to view...
Let p represent a true statement, while q and r represent false statements. Find the truth value of the compound statement.~[(~p ? ~q) ? ~q]
A. True B. False
Subtract.557 - 34
A. 591 B. 423 C. 523 D. 515
Provide an appropriate response.Apply Newton's method to f(x) =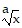 
, a > 0, and write an expression for xn + 1. If the initial guess xo is greater than or equal to 1, what happens to 
as n ? ??
What will be an ideal response?
Solve the problem.A product of two oscillations with different frequencies such as f(t) = sin(10t) sin(t)is important in acoustics. The result is an oscillation with "oscillating amplitude." src="https://sciemce.com/media/4/ppg__tttt0506191043__f1q58g4.jpg" alt="" style="vertical-align: -4.0px;" /> last two functions constitute an "envelope" for the function g(t). For certain values of t, the two cosine functions in g(t) cancel each other out and near-silence occurs; between these values, the two functions combine in varying degrees. The phenomenon is known (and heard) as "beats." For what values of t do the functions cancel each other?
What will be an ideal response?
the product f(t) of the two oscillations as a sum of two cosines and call it g(t).
a graphing utility, graph the function g(t) on the interval 0 ? t ? 2?.
the same system as your graph, graph y = sin t and y = -sin t.