Provide an appropriate response.
Given sets U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4, 5}, B = {2, 4, 6, 8}, C = {5, 6, 7, 8, 9}, find A ? B ? C'.
A. {0, 1, 2, 3, 4, 5, 6, 8, 9}
B. { }
C. {2, 4, 5, 6, 7, 8, 9}
D. {0, 1, 2, 3, 4, 5, 6, 8}
Answer: D
You might also like to view...
Write the system of inequalities that describes the possible solutions to the problem.The Pen-Ink Company manufactures two ballpoint pens: silver and gold. The silver requires 9 minutes in a grinder and 8 minutes in a bonder. The gold requires 11 minutes in a grinder and 8 minutes in a bonder. The grinder can be run no more than 390 minutes per day and the bonder no more than 180 minutes per day. Let x represent the number of silver pens, and let y represent the number of gold pens. Including the system inequalities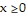 
and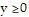 
, find the remaining
inequalities that best represent this company's daily production of silver and gold pens. A. 0 ? 17x + 19y ? 570 B. 9x + 8y ? 390, 11x + 8y ? 180 C. x + y ? 390, x + y ? 180, x + y ? 570 D. 9x + 11y ? 390, 8x + 8y ? 180
Find the slope of the curve at the given point P. y = 2x2 + x - 3, P(4, 33)
A. 15 B. 19 C. 17 D. 5
Solve the problem.A stack of poles has 20 poles in the bottom row, 19 poles in the next row, and so on, with 5 poles in the top row. How many poles are there in the stack?
A. 195 poles B. 177 poles C. 205 poles D. 200 poles
Solve the problem.The economy of a small country can be regarded as consisting of three industries, I, II, and III, whose input-output matrix isIIIIII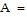 
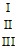
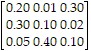Suppose x, y, and z represent the output of industries I, II, and III, respectively. An algebraic expression for the amount of output from industry III that can be exported is
A. z + (0.05x + 0.40y + 0.10z). B. z + ( 0.30x + 0.02y + 0.10z). C. z - (0.05x + 0.40y + 0.10z). D. z - (0.30x + 0.02y + 0.10z). E. none of these