First we show that the statement is true when n = 1.
For n = 1, we get 6
7 = 6
(7∙1) = 6
7This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
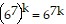
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
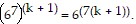
So we assume that
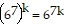
is true and multiply the next term,
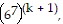
to both sides of the equation.
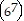 k
k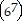 (k + 1)
(k + 1) = 6
7k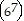 (k + 1)
(k + 1) 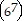 (k + (k + 1))
(k + (k + 1)) = 6
7k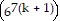
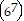 (2k + 1)
(2k + 1) = 6
(7k + 7k + 7)) 6
(7(2k + 1)) = 6
(7(2k + 1))Condition II is satisfied. As a result, the statement is true for all natural numbers n.
 Save a GPA. Donate your notes with us.
Save a GPA. Donate your notes with us.